Chapter 7 - Potato and potahto
Where do little formulas come from?
In chapter 1 we established that if math is a language, then it is for talking about counting, and counting has to do with numbers (eventually written in unary).
We also encountered rules to rewrite a math expression in different ways (in
chapter 5); for example we found out that:
( a + b ) * k = k*a + k*b
where a, b and k are any three numbers.
The "=" sign here does not mean an equation (like it did in chapter 6) but instead that one side is THE SAME as the other.
You might remember these rules from your school math: they were typically called formulas.
The idea here is that you can always replace the left part of a rule with the right (and vice versa too), in any math expression: its look (AKA syntax) will change but not its meaning (AKA the semantics).
Inventing formulas is one of the main things you do when you work with math.
And often formulas come from the fact that you want to count stuff, and that stuff has a structure.
For instance in chapter 1 we wanted to count sequences of Is (or sheep if you prefer) and ended up inventing whole numbers and the base 10 system (abacus and all).
Sequences of tallies have a very simple structure: they are just one I after the other.
In chapter 2 we looked at Peano's definition of numbers, and found that the main characteristic of a whole number is that there can be many Is in it, and that whole numbers come one after the other in single file, so that each one has a successor and predecessor (zero excluded of course). That is a linear structure, like a shopping list, a rather simple, flat structure.
So... what could I count that has a more interesting, more COMPLEX structure than a single file?
What about squares made of matchsticks? For example, one square requires four matchsticks:
But two squares (side by side) only require seven matchsticks:



Interesting... how does this sequence of numbers continue?






It looks like we start from four matchsticks, then add some at every new step. Let's do what Galileo






,


,



, ...





1 sq. 2 sq. 3 sq. ... ↓ ↓ ↓ 4 matches 7 matches 10 matches ...








...
 did (when studying the movement of objects falling to the ground) and look at the differences between one number and the next:
did (when studying the movement of objects falling to the ground) and look at the differences between one number and the next:
| Number of squares | Number of matchsticks | This-Previous |
|---|---|---|
| 1 | 4 | |
| 7-4 = 3 | ||
| 2 | 7 | |
| 10-7 = 3 | ||
| 3 | 10 | |
| 13-10 = 3 | ||
| 4 | 13 | |
| 16-13 = 3 | ||
| 5 | 16 | |
| 19-16 = 3 | ||
| 6 | 19 | |
| ... | ... |
So can I find a math expression that connect the number of squares (call it variable s) with the total number of matchsticks it takes to make that many squares (call it m)?
This expression will work like a kind of machine: the number of squares that I want to build goes in, and out comes the number of matches I need!
Let's go case by case, to get the feeling of things:
when s=2 the machine should reply 1+3+3 = 4+3 = 7,
when s=3 the machine should reply 1+3+3+3 = 7+3 = 10, ...
OK, good. In math (and computer science) they would call the machine a function that defines a RELATION between s and m: numberOfMatchesNeeded( s ) = 1 + 3 * s or for short: matches(s) = 1 + 3 * s. The function definition reads like "the number of matches, that depends on the variable s, is calculated by 1+3*s"; and matches(s) is read as "matches of s".
Terrific. Say that you want to build 5 squares. (spoiler!... according to the table above you would need 16 matchsticks) Using our function, I can calculate how many matchsticks you would need: machtes(5) = 1 + 3 * 5 → 1 + 15 → 16 which is correct. So I can use our function as a SHORTCUT, that tells me how many matchsticks I need to build a certain number of squares, without having to build the actual squares with matches and count. Cool.
And the function itself is our old friend, the linear combination, in this case: one and three times the variable s. In fact, in chapter 2 we played with a linear combination of the form a*10+b and we discovered that "a linear combination can also be a way to re-order, to count numbers in a different order". And in fact here we are using a linear combination in s to count matchsticks in matchsticks squares.
What else could we count? Some stuff with a bit of structure. How about triangles made of dots? Say that I am piling up apples in the window of a shop. A very regular pile could be built step-by-step, and look like these triangles:
•
• • •
• • • • • •
• • • • • • • • • •
where each dot is an apple. I could now ask: "how many apples do I need to make a triangle like that, that has an height of four rows of apples?". And just in case you are wondering, just count the dots in the triangle on the far right in the drawing above... And if I want to be very general in my question, I could ask it like this:
| Triangle's height | Number of apples | This-Previous |
|---|---|---|
| 1 | 1 | |
| 3-1 = 2 | ||
| 2 | 1+2 = 3 | |
| 6-3 = 3 | ||
| 3 | 3+3 = 6 | |
| 10-6 = 4 | ||
| 4 | 6+4 = 10 | |
| 15-10 = 5 | ||
| 5 | 10+5 = 15 | |
| 21-15 = 6 | ||
| 6 | 15+6 = 21 | |
| ... | ... |
The first triangle is just a dot, so height=1. The next triangle has the same amount of dots, and then the height plus 1, which gives me: 1 + (1+1) = 3. The third triangle has the same amount of dots as the second triangle, and 2 plus 1 more, so 3+ (2+1)= 6, and so on:
•
• • •
• • • • • •
• • • • • • • • • •
But look at the last triangle to the right: its height is four, and it has ten apples (AKA dots). Good. Its number of apples can be written like:
1+2+3+4 = 10.
So a triangle of dots (of this kind) that has an height of 4 has:
1+2+3+4 = 10
Is this true for all of our triangles? Sure. In fact:
when height=2 → 1+2 = 3,
when height=3 → 1+2+3 = 6,
when height=4 → 1+2+3+4 = 10,
...
More or less what I need to say is that: tri(n) = addition of all whole numbers from 1 to n or in a more math-like notation: tri(n) = 1 + 2 + ... + n Turns out that these triangular numbers are quite useful, even FAMOUS in math, as they pop up in a lot of different areas. Sum of numbers from 1 to n
Moral of the story so far: math formulas can be created when one needs to count stuff with a structure. For example counting how many apples can be piled up in a triangular mound leads to define a function, that allows to quickly calculate the number of apples needed, give the height of the desired triangle. Some of these functions can be linear combinations.
Double vision
In the previous section formulas come from looking at something from two different points of view. For example the drawing below shows two squares made with matchsticks:
but the drawing also shows seven matches. And since I have these two distinct VIEWS of the same drawing, I can define a calculation machine that expresses the number of matches as a function of the number of squares in the drawing.






As we found out in this book, math it is very important to try and write the same things in multiple ways, eventually ways that look different but really mean the same. It is a kind of double vision in which writing (or drawing) a thing in two or more ways actually does help in finding out more about it.
For instance, consider this square:
Well... I can look at this last expression as an EQUATION, and both sides (to the left and right of the "=" sign) are expressions with the variable n. So I can look back at what we did in chapter 5 (the one about polynomials) and chapter 6 (about equations), and I should be able to see if the two sides of the equation are THE SAME. To do that I need to calculate (AKA simplify) the right part: (n-1)2 + n + (n-1) →
(n-1)*(n-1) + 2*n -1 →
n*n-1*n -1*n+1 + 2*n -1 →
n2 -2*n +1 + 2*n -1 →
n2 and the left part of the equation was n2. So it seems that left and right part of the equation are the same, hence the equation is true. Try for yourself: in the playground below, check that our equation keeps working for large values of n.
The playground might be convincing, but trying with some values (even A LOT of values) is NOT a mathematical proof, and should not be enough to make you completely sure that our equation is true for any whole number n... Luckily, here I have already PROVED that it is, by calculating and showing that the two sides of the equation are equal.
Still! Testing with numbers is a good way to get a FEELING for how this formula works, what it says about the geometry of the sliced-up square.
Now let's look again at the 4 by 4 square, and notice that it can be sliced in other ways too. If I cut it like below:
Again I can try to prove that it is the case, by simplifying a bit both sides of this equation: n2 = (n-1)2 + 2*(n-1) + 1 →
n2 = n2-2*n+1 + 2*n -2 + 1 →
n2 = n2+1 -2 + 1 →
n2 = n2 →
true so squares of dots behave also in this way. Or if you prefer, the dimensions of a square are linked together according to this new formula. And the formula works for squares of any size.
A step back from geometry
OK, so we found a couple of ways to define the area of a square (AKA n2), using a smaller square (AKA (n-1)2) and some other pieces.
But the two equations that we found can also be seen as general rules for re-writing the NUMBER n2.
In fact the two formulas tell me that the square of a whole number like 7 can be calculated without using 7*7 (AKA 72), but using 6 and 62 instead:
n2 = (n-1)2 + n + (n-1) → 7*7 = 6*6 + 7 + 6
n2 = (n-1)2 + 2*(n-1) + 1 → 7*7 = 6*6 + 2*(6) + 1
and (just to be sure) both give 49 as result.
The second formula is even cooler the first, in a way, because it doesn't even use 7, but only 6 and 1! So our second rule saves us time: it allows us to calculate the square of a number, via smaller numbers.
We derived these two formulas from a square of dots (or more precisely from some things that are true about the geometry of squares), but now we want to FORGET that, and focus on what they say about a generic number n, AKA the variable n. And with that in mind, I might ask: looking at the the two formulas as EQUATIONS, will they keep being true also for negative values of n?
Probably not, and not just because I cannot draw a square that has -3 dots on its four side; what worries me is that the left side of each formula is n2, and a negative number to the second power (AKA a number squared) becomes positive, messing up the right parts of the equations.
It's worth trying with -3 for both, just to see what happens. With n=-3 the FIRST equation becomes:
n2 = (n-1)2 + n + (n-1) →
(-3)2 = ((-3)-1)2 + (-3) + ((-3)-1) →
9 = (-4)2 -3 -4 → 9 = 2 →
9 = 16 -7 → 9 = 9 →
true
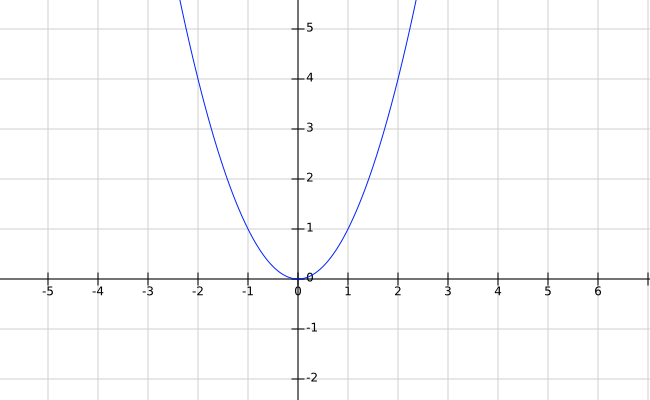
and since I wanted to check if my equation worked for all numbers (positive and negative), one good example is NOT ENOUGH to be sure. So what I could do is to look at a plot of the expression
(n-1)2 + n + (n-1), using FooPlot (like we did in chapter 6).
And because FooPlot works with real numbers, I had to replace n with x, which stands for "any real number"; what I plotted is this slight variation on our expression:
y = (x-1)2 + x + (x-1)
Now I can try the SECOND equation with n=-3: n2 = (n-1)2 + 2*(n-1) + 1 →
(-3)2 = ((-3)-1)2 + 2*((-3)-1) + 1 →
9 = (-4)2 + 2*(-4) + 1 →
9 = 16 -8 + 1 →
9 = 9 → true which means also this equation works for any whole numbers, zero included. Another interesting fact here is that the plot of THIS expression is IDENTICAL to the diagram for the first expression (see above).
In both cases I can drop the restriction, distance myself from the geometrical origin of the formulas, and use them with any value of the variable n.
So when I create my own rules, like
Moral of the story so far: the examples of slicing squares show that it is perfectly OK to make up some weird relationship between certain numbers, and ask "is this true in general?".
Making stuff up
Sice we are working with squares, and we know that we can make up math expressions using examples from geometry, let's consider what happens when there are two squares instead of one.
I could have n2 + m2 and n2 - m2, where n and m are any whole numbers. To keep things simple, let me decide that n is the same or larger than m; it is of course completely arbitrary and all the stuff we will do with these two variables will work even if m was in fact larger, but it will make it easier to draw the squares!
OK, so what can I say about the math expression n2 + m2?
I could try to look at it geometrically, and perhaps start with a couple of concrete values: n=4 and m=3, which gives me 42+32.
The obvious way to calculate this expression is to first find out what 4*4 and 3*3 are, and then add the results, to get 16+9 = 25... but when I work with variables, like n and m, instead of numbers, I cannot do that.
What I can do is try and find a relation between the square of 4 and the
square of 3, and maybe the square of (3+4); that would be interesting.
But how can I write what I SEE in the drawing, in the form of a rule? Well... in this concrete example it should be possible: 72 = 42 + 32 + 2*(a rectangle of sides 4 and 3) →
72 = 42 + 32 + 2*3*4 And the two parts of the rule (left and right) are equal: in fact 72 = 49, while 32+42+2*3*4 = 9+16+24 = 49, so it works! For this particular set of values, 4 and 3, at least.
Now I could be bold and say "I'm sure it will work also in general, for any two numbers, n and m!". If that is true, then the rule becomes: (n+m)2 = n2 + m2 + 2*n*m Fine. But, as we discussed in chapter 5, in math they write polynomials with the variables ordered alphabetically, and also by decreasing powers. Here I can re-organize my expressions so that it becomes: (n+m)2 = n2 + 2*n*m + m2 which is arguably more nice looking, with the powers of n decreasing as I read from left to right, while the powers of m increase.
Potato & potahto. To make sure that the rule above is always true, try to get to it from another, different direction; for instance try using the fact that (n+m)2 is really just (n+m) multiplied by itself.
Do the multiplication, simplify... and see if you get the same as our expression based on the geometry of two squares.
Cheat: look at the solution here
And with that done... We can now BELIEVE that, surprisingly, this equation is true for any values of n and m, including when one or both are negative!
So far so good. Now I would like to look at the expression n2 - m2. Again I could start with two values: n=5 and m=3; only this time I need to built two squares and REMOVE one from the other!
By the way, since I know that I'm calculating 52-32, I might cheat a little and do that calculation... and the result is 25-9 = 16 dots. So the total dots in all the pieces, after cutting a MISSING square out, should be 16.
But... without cheating, I could add up the areas of the two blue rectangles and the orange square: 52-32 = 2*(5-3)*3 + (5-3)*(5-3) →
16 = 12 + 4 →
16 = 16 So the general case should look like this: n2 - m2 = 2*(n-m)*m + (n-m)2 This rule is true for any n and m, because the left and right part of the formula are equal. Moreover, from it I can even derive a rule for (n-m)2: n2 - m2 = 2*(n-m)*m + (n-m)2 →
-(n-m)2 = 2*(n-m)*m -(n2 - m2) →
(n-m)2 = -2*(n-m)*m + n2 - m2 →
(n-m)2 = n2 - 2*(n*m-m*m) - m2 →
(n-m)2 = n2 - 2*n*m + 2*m2 - m2 →
(n-m)2 = n2 - 2*n*m + m2 The last equation is really the same as our old friend: (a+b)2 = a2 + 2*a*b + b2 only when b is a negative number. In fact: (n-m)2 = n2 - 2*n*m + m2 →
(n+ (-m) )2 = n2 + 2*n*(-m) + (-m)2 So now we also have learned about two different roads, both leading to (n-m)2. One gets there via (n2-m2), and the other via (a+b)2. Interesting.
OK, but back to our difference of squares. There is at least another interesting way to reorganize the parts of our squares:
52-32 = 5 * (5-3) + 3 * (5-3) →
16 = 5*2 + 3*2 →
16 = 16 so this new rule is also correct (for this particular case with n=5 and m=3), even if it is very differnt from the previous one. And in the general case this one will look like this: n2-m2 = n * (n-m) + m * (n-m) which can be written in a nicer way (by putting together the two (n-m) expressions): n2-m2 = (n+m)*(n-m) This last formula is famous: it is usually called difference of two squares in school math, and it is a member of the family of the "special products".
An interesting thing about this formula is that it turns a subtraction into a multiplication (see the relations among operations in chapter 3), a rather unusual rewriting! Consider what that looks like with numbers: 16-9 = (4-3)*(4+3) →
1*7 → 7 or even: 12-7 = (√12-√7)*(√12+√7) →
(3.464-2.646)*(3.464+2.646) → 0.818*6.11 → 5 And finally, this rule works also with variables and math expressions: 16*x2-49 = (4*x-7)*(4*x+7) And in this book we have not discussed how to solve equations with x2 (AKA second order equations), but a simple example could be a question like "what value or values of x make the expresion 16*x2-49 become 0?". In math terms we should write: 16*x2-49 = 0 and then look for a solution of the form x=SOMETHING... and it is difficult to SEE what that SOMETHING should be. I could try a few values of x, like we did in chapter 6, or plot the expression to see how it looks. But here I know that this is a difference of squares, so I can just rewrite the equation as: (4*x-7)*(4*x+7) = 0 and the good thing about this is that it says "something * somethingElse = 0", and that must mean that if the something or the somethingElse are zero, then the equation is satisfied. So instead of one second order equation, I have to solve two linear equations in x: a much simpler task! (4*x-7) = 0 (4*x+7) = 0
4*x = 7 4*x = -7
x = 7:4 x = -7:4
x = 1.75 x = -1.75 And that tells me that when x is -1.75 the equation is true, but also when x is 1.75... so this equation has two solutions. In the previous chapter we said that linear equations can have zero, one, or infinite solutions; well, turns out that second order equations can have zero, two, or infinite solutions. Sometimes the two solutions can be identical, then we could say that they are one solution.
To get a better feeling about this equation I plotted it (using FooPlot). The diagram below is the plot of the equation, rewritten as y = 16*x2-49.
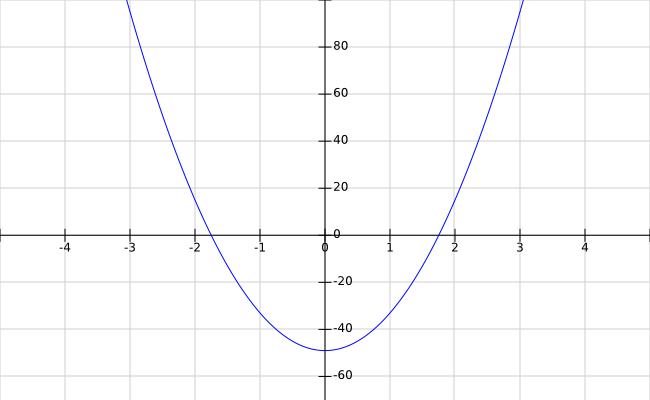
So, thanks to the difference of squares rule we can EVEN solve some types of second order equations... not bad. However, this technique for solving equations in x2 does not work for ALL second order equations, but when it works it is pretty quick and useful.
Problems within problems
Formulas can also be created when a variable is substituted by an entire expression.
Wait... when would that be needed? Putting a math expression in the place of a variable?
Well, it could make sense if a problem is based on another problem.
For example, consider the problem of finding out how many matchsticks I need to build a certain number
of squares (that we solved in the beginning of this chapter).
We didn't only solved that problem, we also created a SEQUENCE of numbers: the numbers
generated by the matchsticks squares. The first matchsticks square used 4 matches, the second used 7, then 10, and 13, and so on.
So the sequence generated is: 4, 7, 10, 13, ....
Say that I have new problem, and that I need to use that sequence to solve it.
The problem could be that I want to build a lot of dots squares, with sides based on the sequence above. And I am interested in finding a function that would give me the area of one of these dots squares, given its index in the sequence. Here is a visual representation of the situation:
4 matches 7 matches 10 matches 13 matches ...












... ↓
Area = 16
Let me be more concrete. The smallest of these new squares should have side equal to 4, and an area of 4*4 = 16; the second's side should be 7, and the area 7*7 = 49. Then a side of 10, and an area of 10*10 = 100, and so on.
In general, to know the area of one such square, I need to take n, calculate the nth number in the matchsticks sequence, and then calculate its square.
We found the function that gives the matchsticks sequence numbers, given s, and it was: matches(s) = 1 + 3 * s OK, but here s should really be called n. So I can substitute s with n, and get: matches(n) = 1 + 3 * n Fine. Now, I want to call the new function squaresOfSquares, and I expect it to be of the form something2, because... after all we are measuring areas of squares in this new problem. But what should the variable something be? What about the result of matches(n)?! I can try to substitute the variable something with matches(n): something2 → matches(n)2 → (1+3*n)2 Good, so the result is a function like this: squaresOfSquares(n) = (1+3*n)2 This squaresOfSquares(n) function takes a number n and gives back the area of the square of dots, that has the sides of lenght matches(n). Interestingly, this new function is made up of two other functions composed together. Let's to get an idea of how this function works:
| n | squaresOfSquares(n) |
|---|---|
| 1 | 4*4 = 16 |
| 2 | 7*7 = 49 |
| 3 | 10*10 = 100 |
| 4 | 13*13 = 169 |
| 5 | 16*16 = 256 |
| ... | ... |
OK... and what is the MEANING of this function? Well, the function squaresOfSquares(n) answers the question "what is the area of a certain square?", or if you like "how many dots are in a square with a side based on the sequence of matchsticks squares numbers?".
What the table above shows are a few results of the function squaresOfSquares(n), for some input values for the variable n.
In math terminology, writing someFunction(5) means that the function someFunction(k) is CALLED with the value 5 substituted to the input variable k. So in math you can say something like "I am CALLING a function with some input value".
More precisely, if the function someFunction is defined like this: someFunction(k) = some math expression involving the variable k then the result of calling someFunction(5) is to substitute the variable k in the defintion with the value of the CALL, here 5. So it becomes: someFunction(5) = some math expression involving the constant 5 When calculated, a function call is going to become a number; in this example someFunction(5) might turn out to be the number 123, and that is fine. But it also mean that I can treat the call to a function as an un-calculated number, another example of the lazy evaluation approach that we discussed in this book. If you are with me so far, then you should agree that it is OK to write something like: someFunction(5)+5 or: 12*someFunction(5) or: 99 + someFunction(a) + someOtherFunction(b) or even: someFunction( someOtherFunction(a) + b ) * 99 where a and b could be numbers or variables. So function calls can be mixed in with all the other math entities we have encountered so far, such as whole and broken numbers, negative numbers, fractions, variables and linear combinations.
Finally, I find it also very interesting to see that even a function can be written in multiple ways, all having the same meaning. For example we just used the fact that:
matches(s) = 1+3*s
is THE SAME as
matches(n) = 1+3*n.
I just have to be sure that the new variable n is not present in the original function, otherwise I would mess things up.
We even COMPOSED two functions togehter, a new operation that makes sense only with functions:
squaresOfSquares(n) = (1+3*n)2
which can be seen as these two machines (AKA functions):
a --> [ a2 ] --> squareOfN
connected together. And the result is a new, LARGER machine, that uses both to calculate my new function squaresOfSquares(n):
j --> [ j+j+j3 ] --> anotherResult
A square peg in a round hole
We have made up a few math rules in this chapter. For example:
(n+m)2 = n2 + 2*n*m + m2
n2-m2 = (n+m)*(n-m)
But when should I use a math rule (AKA formula)? Well, is not difficult to decide: for example when
I have two variables and I need to calculate their square, I can use the first of the two formulas above.
If I have three apples and four bananas to SQUARE, AKA (3*apple+4*banana)2, I can just
substitute n with 3*apple and
m with 4*banana and follow the rule:
(3*apple+4*banana)2 = (3*apple)2 + 2*(3*apple)*(4*banana) + (4*banana)2
automatically, without even thinking... typographically if you like.
The of course then I will have to do a few calculation, to make my result LOOK a bit better:
9 * apple2 + 2*3*4 * apple*banana + 16 * banana2 →
9*apple2 + 24*apple*banana + 16*banana2
In cases like this I'm using a rule left-to-right, or forward, and all I have to do is to substitute my expressions to the original variables of the formula (and perhaps calculate a bit, to
clean up). This is not very different than what we discussed above about calling a function.
Fine. But what about the other way around? What about this: take a long expression and look for a way to FIT IT in a certain template; then use a rule and rewrite the original expression.
Confused? Sorry. Let me find an example.
Say that you are trying to solve a problem, and after writing your problem down as a math expression, you are left with this: 9*x2 + 12*x + 4. And for some reason you would very much like to rewrite that as the square of something, AKA (something)2, where your
something is possibly a math expression that contains x.
Thanks to the rules we have found in this chapter, you know that something like
n2 + 2*n*m + m2
can in fact be rewritten like (n+m)2. For sure.
So... how do you fit your "square peg" 9*x2 + 12*x + 4 into the "round hole"
n2 + 2*n*m + m2 ? Do these two expression even match?
And assuming things fit, and you can rewrite your initial expression as
(n+m)2, what would n and m be here?
Well, to use a formula backward I need to change the look of an expression until it looks like another expression; and all the transfromations that I will use in the process, should not change what the first expression meant. (Sounds familiar? Like when we discussed normal forms in chapter 1 or chapter 6...? Just saying...)
So how can I make 9*x2 + 12*x + 4 look like
n2 + 2*n*m + m2 ?
Well, luckily they are not VERY different to begin with!
Unless I can "see" how to rewrite the first expression to have the same shape, or form, as the second, I might take an experimental approach: try and MUTATE the first expression, see in how many ways I can re-write it without changing its meaning, then find the look that seems more promising to have a close match with the second expression.
Finally, I can try to fit the MUTATED expression in the template (AKA the second expression, AKA the "round hole").
OK then, let's play this mutation game:
| 9*x2 + 12*x + 4 ⇙ ⇓ ⇘ |
||
| split into factors
3*3*x*x + 2*2*3*x + 2*2 |
||
| group x
x*(9*x + 12) + 4 |
||
|
smtg + smtg + smtg
(9*x2) + (12*x) + (4) |
OK, let's say that this one (9*x2) + (12*x) + (4) is interesting, it has potential to become n2 + 2*n*m + m2. I can now try to match some parts of the first with some parts of the second:
| 9*x2 | + | 12*x | + | 4 |
| ⇓ | ⇓ | ⇓ | ||
| n2 | ? | m2 | ||
| ⇓ | ⇓ | |||
| n2=9*x2 → | m2=4 → | |||
| n = 3*x | m = 2 |
Good. Now I know that n=3*x and m=2, but I NEED also 12*x to have the same shape as 2*n*m. So I can try going up this time!
| 9*x2 | + | 12*x | + | 4 |
| ⇓ | ||||
| 12*x | ||||
| ⇑ | ||||
| n = 3*x ⇒ | 2*n*m = 2*(3*x)*2 | ⇐ m = 2 |
Bingo! So the matching is possible, and the way things match tells us how to rewrite our expression: (9*x2) + (12*x) + (4) → ( 3*x ) 2 + 2*( 3*x )*( 2 ) + ( 2 )2
And now that I know what n and m should be to match the template, I can finally use the rule: (n)2 + 2*(n)*(m) + (m)2 = (n+m)2 → (9*x2) + (12*x) + (4) = (3*x+2)2 So now the square peg fits the round hole! And my expression can be re-written as: (3*x+2)2 Great. Our experimental approach paid off: now we know a possible way to fit an expression into a template. And that means we know how to use a rule right-to-left, or backward if you like.
Another misfit
Now we have a technique to FIT an expression into a template, and that allow us to use the math rules that we have discovered forwards and backwards. Cool.
Let's test this new idea of fitting an expression to a template, with another square:
( egg + salt + bacon )2
which represents a breakfast square?! Or if you remember the fruit salad interpretation of multiplication, from chapter 5, then this could be seen as a combination of breakfast ingredients to create a new menu...
And if you like a simpler example, it is the same as asking how to calculate (a+b+c)2.
But regardless... what should we do here? After all our rule works when there are TWO variables
(n+m)2.
How can I put 3 feet in 2 shoes? Because that's what ( egg + salt + bacon )2 looks like, with respect to the template (n+m)2.
What are n and m here? When I have three things, egg, salt and bacon!
Perhaps I can CHEAT a bit and group two things, and pretend I only had two to start with... But would it work? Let's see:
( egg + salt + bacon )2 → ( (egg+salt) + bacon )2
OK, so now it is of the form:
( someThing + someOtherThing )2
which is promising. I can now use the rule and see where it gets me:
( (egg+salt) + bacon )2
→
n2 + 2*n*m + m2
and after substituting n and m with our expressions and variables, it becomes:
(egg+salt)2
+ 2*(egg+salt)*bacon
+ bacon2
OK, it worked! Now I can calculate a bit further
(egg+salt)2
+ 2*(egg+salt)*bacon
+ bacon2
→
(egg+salt)2
+ 2*egg*bacon + 2*salt*bacon
+ bacon2
And now I have ANOTHER SQUARE to calculate, because the first part of the expression,
(egg+salt)2, fits nicely in the SAME template, so I can use the same rule again, with a different choice of n and m this time:
( egg + salt )2 →
n2 + 2*n*m + m2 &rarr
egg2 + 2*egg*salt + salt2
Putting it all together:
(egg2 + 2*egg*salt + salt2) + 2*egg*bacon + 2*salt*bacon + bacon2
and I just have to clean it up:
egg2 + salt2 + bacon2 +
2*egg*salt + 2*egg*bacon + 2*salt*bacon
Done. And it looks very elegant. We knew that "the square of two terms (n+m) is the sum of each squared, and their double product".
And we just found that "the square of three terms (a+b+c) is the sum their squares, and their double mixed products". I was not expecting this, and it even has a nice structure to it.
Note: eggs, salt and bacon really is a powerful combination!
Fine. We can conclude by making more stuff up about how to write a thing in multiple ways. We can in fact define a rule about all this:
(a+b+c)2 = a2 + b2 + c2 + 2*a*b + 2*a*c + 2*b*c
And if you like potato (or (a+b+c)2) and I like potahto
(or a2 + b2 + c2 + 2*a*b + 2*a*c + 2*b*c)...
let's call the whole (math) thing off!
Puzzles
(1) Make up a formula.
Consider these (very modern art-looking) matchsticks trees:














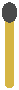
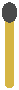
 ,
, 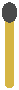 ,
,  ,
, 
If you only count the unused matches (those with a red head), you will find that they define a sequence of numbers: 1, 2, 4, 8, and so on.
Can you find a function to count these trees? Let's call this function leaves(lev), and the idea is that it answers the question "how many leaves does a matchsticks tree have, when it is lev levels tall?".
To help you get started, let me write down a few observations:
- the first tree (from the left) has 1 leaf and is 1 level tall
- the second tree has 2 leaves and is 2 levels tall
- the third tree has 4 leaves and is 3 levels tall
The definition of you function should look something like this: leaves(lev) = some math expression involving the variable lev
(2) Formulas and geometric shapes
Consider three numbers 5, 2 and 3. I want to use the first number to draw a square with side 5:
Counting the dots in the last drawing I can see that the area of the large square is (5+2)*(5+3), which gives 7*8 → 56 dots. Fine, but instead of calculating the result, I want you to "look" at the shapes and find a way to express the multiplication as an addition of area of rectangles... Find another way to write: (5+2)*(5+3) = ? so that the right part of the formula takes into account the various rectangles in the drawing above.
When you have done that, for this particular three numbers 5,2 and 3, generalize your formula to work for any three numbers x, a and b: (x+a)*(x+b) = ?