Chapter 6 - Riddles and answers
Create a riddle
Say that I want to create a riddle (about numbers, just because...). I could start with the stupidest riddle ever and say: "I have some sheep. The number of sheep is 5. How many sheep do I have?".
Not an impressive challenge... but wait. I can do better, by transforming a bit my riddle, for example I could multiply everything by ten. That would give me:
= "10 times the number of sheep is 50"
What else could I do to make my riddle more interesting? Add something perhaps. Let's see:
= "10 times the number of sheep and 4 is 54"
Interestingly, these two types of transformations work on different parts of the sentence. The transformation "time k" changes a riddle in this way:
Let's try applying a few more transformations to my riddle:
= "20 times the number of sheep and 8 is 108"
= "20 times the number of sheep and 9 is 109"
= "20+1 times the number of sheep and 9 is 109+5"
= "21 times the number of sheep and 9 is 114"
So to create a good riddle, I could start by a stupid one "I have 5 sheep", then make it more and more complex-looking (but the meaning, the semantics, stays the same!) using three kinds of transformations: *k, +n, and +sameNumberOfsheep. And for example I could ask you: "I have some sheep. 21 times the number of sheep and 9 is 114. How many sheep do I have?", and that would be much more FUN for you to solve.
Click START again to reset the riddle. Now try using a short random sequence of transformations... could you solve that riddle? How?
Change the number of sheep to 0, and click START again. Apply the following transformations, one after the other: *3, +1, +sheep, +sheep. Can you solve that riddle? Verify that 0 is the answer.
Moral of the story so far: the simplest possible riddle IS its own solution here; and every difficult riddle is just a simple riddle made to LOOK more complex, by transforming it multiple times.
Solve the riddle
However, this idea of going backwards from an answer to a riddle, using a transformation after another is very general in math, and it is even more interesting when you imagine the process inverted. Could I take a riddle, transform it and transform it, until I eventually get an answer?
As an example I could try to solve: "10 times the number of sheep and 4 is 54"... but where to start?
I can look at the two main types of transformations I used to build this riddle:
- *k , multiplication by a number (any number, positive or negative, or fraction, just not zero)
- +n , addition of a number
That sounds like a bold statement... let's be sure that it is true, before we continue. Say that I start again from the simplest riddle (AKA an answer) "the number of sheep is 5", then I multiply this riddle by 10 like I did in the previous section, and get: "10 times the number of sheep is 50". I can REVERSE this transformation, by dividing by ten: ("10 times the number of sheep is 50"):10 →
"1 times the number of sheep is 5" and all I had to do was to use the SAME transformation, but multiply by the inverse of ten, which is 110.
Can do the same for the addition-type transformations? Again, let's see on the example:
= "the number of sheep and 4 is 9"
= "the number of sheep is 5"
Note: we covered inverse and opposite numbers in chapter 3.
Now I can try again with: "10 times the number of sheep and 4 is 54". Here the interesting numbers are 10 and 4. I could start with one of two things: divide by ten or subtract four. Say I start dividing by ten:= "the number of sheep and 0.4 is 5.4"
"the number of sheep and 0 is 5" =
"the number of sheep is 5"
The other alternative is start by subtracting four:
"10 times the number of sheep and 0 is 50" =
"10 times the number of sheep is 50"
"the number of sheep is 5"
Experiment with a few riddles, to see what happens when you transform them.
Did you notice anything about the two kinds of transformations, playing with the playground above?
What? Perhaps something about the order in which you decide to apply the transformations and the precision of the calculations?...
Navigation tricks
When you play with the playground above, it seems that it is possible to find the answer in two steps, every time. Cool.
But can we be sure that it is the case EVERY time? For us, every riddle is a sentence of the form:
"a times the number of sheep and
b sheep is c".
Now, consider the special cases: "0 times the number of sheep is 5", and
"0 times the number of sheep is 0".
The first riddle has no answer: it is IMPOSSIBLE for a number MULTIPLIED by zero to become five.
The second riddle is different. What number of sheep would make the sentence true?
I can try with 1 and I will get "0 times 1 is 0", which is true.
And what about 2?
Well, "0 times 2 is 0" is also true... and so with ANY number. So this riddle has INFINITE answers, because any number of sheep will satisfy it.
Fine, I will have to look out for those two special cases... but for all other cases it looks like I can solve the riddle in two steps. So here we have a procedure that starts from a riddle sentence, and following two steps, always gives me the answer to the riddle (eventually treating the two special cases in a different way). Now: a procedure that starts from some data about a problem, and follows a specific number of steps to always produce the answer to that problem, is called an algorithm.
The word "algorithm" comes from the name of al-Khwarizmi  a Persian mathematician, astronomer, geographer; according to Wikipedia:
Al-Khwarizmi's popularizing treatise on algebra (The Compendious Book on Calculation by Completion and Balancing, c. 813–833 CE) presented the first systematic solution of linear and quadratic equations.
Spoiler: our riddles are what math calls "linear equations" or "first degree equations"!
a Persian mathematician, astronomer, geographer; according to Wikipedia:
Al-Khwarizmi's popularizing treatise on algebra (The Compendious Book on Calculation by Completion and Balancing, c. 813–833 CE) presented the first systematic solution of linear and quadratic equations.
Spoiler: our riddles are what math calls "linear equations" or "first degree equations"!
So playing with the playground above we have actually found an algorithm for solving any of our riddles! Terrific. Let's write down clearly and step-by-step how the algorithm works:
-
take a riddle written like: "a times the number of sheep and
b sheep is c";
for example: "10 times the number of sheep and 4 sheep is 54". -
use a transformation to subtract whatever number b is, getting
a simpler riddle of this form: "a times the number of sheep is
(c-b)";
in the example the transformation is add -4, and the result is:
"10 times the number of sheep is 50". -
then use another transformation to divide by a, getting:
"the number of sheep is (c-b):a";
in the example the transformation is multiply by 1a: "the number of sheep is 50:10", or "the number of sheep is 5"!
The no solution cases all look like: "0 times the number of sheep is c", so I need to execute my algorithm (AKA "run" the algorithm) on a=0 and b=0, and any number I like for c. However, c should not be zero, because if it was then this case will become the other case, the one with infinite solutions. Following our algorithm I get:
On the other hand, the cases with infinite solutions all look like: "0 times the number of sheep is 0", so I have to run the algorithm on a=0, b=0, and c=0 too. And in this case I get:
Those two kinds of cases are a problem for my algorithm because a procedure to calculate something is NOT an algorithm if it can get STUCK even in a single case. And here I have two "families" of riddles that would make my algorithm stuck... not good.
So to avoid my algorithm to get stuck I have to write it better, so that the steps are more solid, and I can avoid the trap of these two special cases. Here is the correct algorithm to solve linear equations (AKA any of our riddles):
-
take a riddle written like: "a times the number of sheep and
b sheep is c"
- In case a, b and c are all 0, then stop and answer "any number of sheep would do for this riddle".
- In case a and b are 0, but c is not, then stop and answer "there is no solution to this riddle".
- transform the riddle to "a times the number of sheep is (c-b)";
- transform again to get "the number of sheep is (c-b):a", the answer to the riddle.
Two-pan balance
First of all, let me tell you that in math the variable x is traditionally used to stand for thing we don't know (for example the amount of sheep, in our riddles) mainly for historical reasons. Adopting this convention, I could change the way I write my riddles, from: "2 times the number of sheep and 1 is 3" to something like this:
OK, then I think I will rewrite my riddle to look like this: "2 times x and 1" = 3. Spoiler: the solution to this riddle is x=1, because 2* 1 +1 is equal to 3.
A way to SEE what is going on in our riddles is to draw a two-pan balance, and place each part of a riddle on one of the pans. The result looks like this:
Let's take another riddle, for example "10 times x and 4 sheep" = 54, and see how that would look drawn as a two-pan balance.
Another interesting transformation that makes sense with the two-pan balance is to add or remove x from both pans. If I add x to both pans I get:
Now I can go back to my solution x=5 and subtract x instead. I get:
Now, if the two pans are the same, I can SWAP THEM AROUND, and the two-pan balance will still be in... balance. So I could draw this instead:
OK, so riddles like "2 times x sheep is the same as 5 and x sheep", are a "new" format, and what I find very interesting about them is that they look like a comparison of two linear combinations, involving the variable x.
As we have found out in the previous chapter, a linear combination with numbers and the variable x is something like a*x+b, where a and b are some numbers. And here my riddle can be written like:
And the fact that I can draw any riddle as some weights on the two pans of a balance, fits very well with the realization that a riddle is an equivalence of two linear combinations. And thanks to what we did in chapter 5, I even know how to calculate stuff like:
or (2*x) : 10 = ??
or (2*x) -x = ???
Go back to chapter 5 if you need to look up the rules for addition and multiplication for linear combinations.
And now let's play with the playground below.
Apply the transformations in reverse to get back to x=5.
Now: change the value of x to zero, which means "1 times x and 0 is 0". Then click START to reset the riddle; multiply by two and by three a few times. What happens to the two pans of the balance?
Finally, experiment a bit with the two-pan balance. Set x to -1, so "1 times x and 0 is -1" and restart; see if you can find the shortest way to get to:
"1 times x and 3 is the same as 0.5 times x and 2.5".
Before moving away from the two-pan balance, I would like to see how the two special cases ("no solution" and "infinite solutions") look in this representation.
Starting from the case with no solutions, which is a riddle of the form
"0 times x and 0 is c", I get this drawing:
The case with infinite solutions looks like this: "0 times x and 0 is 0"; and the two-pan balance is:
"0 times x and 0 is 2", and "0 times x and 0 is 0".
Note that in the case with infinite solutions, any riddle you build says something totally obvious and not helpful in finding out what number x should be... For instance, I starting from "0 times x and 0 is 0" you can easily get
Moral of the story so far: riddles (AKA linear equations) can be written as sentences about sheep or drawn as two-pan balances, with specific weights on the pans; but a riddle is also an equivalence between two linear combinations, both potentially with the variable x. We have an algorithm to solve these equations, and there are two special cases we have to watch out for. We also discovered that there are only three possible types of answers for a riddle: zero, one or infinite solutions.
But what about the real world?
In your school math lectures you might have encountered equations in a very different context: not as riddles, but as a way to express and solve "real life" problems.
And now that we have looked at the two-pan balance, we can too. Take a situation where you have a lot of bricks (identical bricks, same size and weight) and would like to know how much a brick weights. But the only thing you know is that when you put three bricks on one pan, you have to put one brick and eight kilograms on the other to balance them.
What is the riddle (AKA equation) that represent that situation?
It should be:
Good, but having to draw all these two-pan balances is a bit too much work... it would be much more productive to have a SHORTER way to write down these equations and the steps needed to solve them.
Write this stuff shorter
Time to write this stuff shorter, drop the sentences and the balances, and focus on the linear combinations (AKA polynomials), and invent a good normal form for an equation. And since we are at it, let's also define properly what the meaning-preserving transformations are in this case, and how they can change an equation.
What can I use for as normal form for an equation?
I would like to go back to the interesting fact that a solution to a riddle is a (simpler) riddle. Therefore, a good normal form for an equation should be its solution: x=5, for example!
But, wait... what a surprise! This is a linear combination of x and am I saying that it must be the same as (AKA equal to) an ordinary number: 1*x=5. We can use the same notation we invented in chapter 5 to represent math expressions with variables, the labeled boxes, and write the equation 1*x=5 as:
x1│ 5
and I will have to remember that these two boxes contain each a linear combination of x and some numbers, and that the left and right box must be kept EQUAL for the equation to make sense.
OK, and if that is the normal form, it means there are alternative ways to write the SAME thing (as we discussed already in chapter 1, about whole numbers and abacus-numbers).
We have already used some transformation on riddles, like: multiply by a number, add a number,
add x.
But since we are talking about linear combinations now, I can do those things and better (and more general) stuff too:
- multiply both linear combinations (left and right of the "=" sign) by a non-zero number k.
For example: (1*x=5) *10 → (1*x) *10=(5) *10 → 10*x=50, where k is 10,
or if you prefer the boxes: (x1│ 5) *10 → (x1*10│ 5*10) → (x10│ 50) - add the same number to n to both sides of the equation,
for example: (1*x=5) +10 → (1*x) +10=(5) +10 → 1*x+10=15,
or with the boxes: (x1│ 5) +10 → (x1│ 15) - add k-time x to both sides of the equation, where k is any number.
Example: (1*x=5) +2*x → (1*x) +2*x=(5) +2*x → 3*x=5+2*x
Boxes: (x1│ 5) +x2 → (x3│x2 5) - add a linear combination in x that looks like m*x+n to both sides of the equation.
Example: (1*x=5) +(2*x+3) → (1*x) +(2*x+3)=(5) +(2*x+3) →
(1+2)*x+3=2*x+3+5 → 3*x+3=2*x+8
Boxes: (x1│ 5) +(x2 3) → (x1x2 3│ 5x2 3) → x3 3│x2 8 - swapping the two sides is also OK.
Example: 1*x+5 = 2*x+3 → 2*x+3 = 1*x+5
Boxes: x1│ 5 → 5│x1 - move something from one side of the "=" to the other is also possible, and it changes the look but not the meaning of the equation.
Example: 1*x+5 = 2*x → (1*x+5) -1*(2*x)=(2*x) -1*(2*x) → (1*x+5)-2*x=0 → ect.
Boxes: x1 5│x2 → (x1 5│x2) -x2 → x1-2 5│ 0 → x-1 5│ 0
So the short answer is: to move something from side to side, just flip its sign.
1*x*2*x + 1*x*3 = 5*2*x + 5*3 →
2*x2 + 3*x = 10*x + 15
2*x2 + 3*x -10*x - 15 = 0 →
2*x2 -7*x -15 = 0
which is perfectly fine as a polynomial in the variable x. But because the variable x is present as x2 as well, this is no longer a linear equation in x, but it is now an equation of second order in x, a DIFFERENT KIND of riddle altogether, and we would need our friend al-Khwarizmi
 to be able to solve those!
to be able to solve those!
OK, then perhaps for now it is better NOT to multiply a linear equation by a linear combination that contains x... to avoid jumping outside the world of linear equations and into more complicated kinds of equations.
Finishing the algorithm
Now we can look back at our algorithm to solve linear equations (AKA riddles).
It works fine, but it requires the equation to be in the form
"a times the number of sheep and
b sheep is c";
however, we have extended the way we write equations, to include equations that are made of two linear combinations, one on each side of the "=" sign. Our algorithm cannot cope with those yet.
Time to finish the algorithm, so it can solve any kind of linear equations in x!
The idea here is to add a step in the very beginning of the old algorithm, to rewrite the equation into the nice form "a times the number of sheep and
b sheep is c", then
simply continue with the rest of the old algorithm (which worked just fine).
So if I have an equation like this:
1*x+5 = 2*x+3 the smartest thing to do is to move all the x-related stuff to the left and all the ordinary numbers to the right.
In this way my equation will FIT a form that my algorithm can work with!
Here I get: 1*x-2*x = 3-5, thanks to the rule that says than when things move across the "=" sign, their sign flips.
And you might have realized by now that moving terms across the "=" is not really a NEW transformation,
but rather a clever use of an add n transformation, only that n here is chosen to be the opposite of the term that I want to move; for instance:
1*x + 5 = 2*x + 3
⇓ -2*x
1*x + 5 -(2*x) =
2*x + 3 -(2*x) →
1*x + 5 - 2*x = 3
Good. Now I can calculate a bit on each side:
1*x-2*x = 3-5 →
-1*x = -2
And finally I can divide both sides of the equation by -1 (because it is the number that multiplies x in the left part of the equation), and get:
(-1*x):(-1) = (-2):(-1) →
1*x = 2
And that's the solution of the equation, or if your prefer its normal form.
Generalizing from this example (but also keeping in mind the two special cases), our revised algorithm to solve linear equations is:
-
take a linear equation written like: i*x + j = m*x + n and move stuff around until you get something that looks like
a*x=b
- In case a and b are both 0, stop and answer "any number is a solution to this equation", or "this equation has infinite solutions".
- In case a is 0, but b is not, stop and answer "there is no solution to this equation".
- transform the equation in this form: x = (b:a), and ba is the solution.
-
start by: 1*x+5 = 2*x+3. It needs cleaning up, so move stuff around:
1*x+5 -2*x =
2*x+3 -2*x →
1*x+5 -2*x -5 = 2*x+3 -2*x -5 →
1*x-2*x = 3-5 →
-1*x = -2 Now looks like a*x=b, with a=-1 and b=-2.- Are a and b both 0? Nope... then go on.
- Is a equal to 0? No... go no.
- The soltuion is ba, and here that is -2-1 → x=2.
Tables and drawings
OK, so by now it is clear that an equation is the equivalence of two linear combinations (in the variable x).
For example I know that the solution of 1*x+5 = 2*x+3 is x=2, and that must mean that if I were to replace every COPY of the variable x in both linear combinations with the number
2, I would get the same result on both sides. (In math they call this replacement "a substitution".)
Let's see, when x=2 the equation becomes:
1*(2)+5 = 2*(2)+3 →
2+5 = 2*2+3 →
7 = 7
which is true; so I can say "the value 2 SATISFIES the equation", or
"the value 2 makes my equation true".
You can try with any other number, but ONLY 2 will satisfy this equation. After all we discovered before that a linear equation can have zero, one or infinite solutions; this one has one solution, and only one. Let me show you, for example with x=0 (also because zero makes the calculations simpler!):
1*(0)+5 = 2*(0)+3 →
0+5 = 0+3 →
5 = 3
which unfortunately is false; hence, x=0 cannot be the solution... and I knew that.
However, this idea of TESTING is interesting. I could try substituting x by a few numbers, and hopefully get an some hints of the solution of the equation.
The same is true if we use a nicer form for the equation: a*x=b. In our example that would be: -1*x=-2. The table in this case would look something like this:
| x | -1*x | -2 | Equal? |
| 0 | 0 | -2 | false |
| 1 | -1 | -2 | false |
---> | 2 | -2 | -2 | true | <---
| 3 | -3 | -3 | false |
And here we are comparing -1*x with -2, but -2 is still a polynomial in
x, because -2 can be written in another way too: 0*x-2.
OK, it looks like searching for the solution to an equation can be done by writing a table, a very long and fine-spaced table, to find that ONE NUMBER, by which the two columns (left and right part of the equation) are the same. Good plan... however, we might be end up with a very, very find-spaced table!
For example take this simple-looking equation: 1000*x+7=130. Using our algorithm we can immediately find the solution: 1000*x=130-7 → 1000*x=123 → x=0.123. But finding this value in the table would mean calculating A LOT of rows, with a very small "step" between two calculations. Difficult, but... let me try, starting from -1:
| x | 1000*x+7 | 130 | Equal? |
| -1 | -993 | 130 | false |
| 0 | 7 | 130 | false |
| 1 | 1007 | 130 | true |
Since the column |1000*x+7| is clearly growing too much already, it is useless to look after x=1; for a similar reason, it makes no sense to look for values of x before 0, since the column |1000*x+7| goes negative and will continue to get more negative (AKA a larger number with the "-" sign in front). Remember that our goal is to find a value of x where the number in the column |1000*x+7| is THE SAME as the next column, AKA is equal to 130.
And from this little bit of table that I calculated, it looks like the two columns ARE in fact equal, somewhere between x=0 and x=1... but where? Time to ZOOM IN! Let's look at the interval between 0 and 1 in more DETAIL, AKA with a smaller step. Instead of going from x=0 to x=1, I need to go x=0, x=0.1, x=0.2, ect. with a step of 0.1 instead of my previous step of 1.
| x | 1000*x+7 | 130 | Equal? |
| 0 | 7 | 130 | false |
| 0.1 | 107 | 130 | false |
| 0.2 | 207 | 130 | false |
And again I should stop at x=0.2 because I already overshoot the target of 130; the solution must be between x=0.1 and x=0.2, and even x=0.1 is a decent APPROXIMATION to the solution. Is NOT the RIGHT solution, but it looks better than my previous "guess" x=0.
I could ask at this point "how much WRONG is x=0.1" as a solution to 1000*x+7=130? And I can calculate that; I just need to use the equation written like 1000*x=123, and substitute x with 0.1. In this way I get: 1000*0.1=123 → 100=123 which is false... but PRETTY CLOSE! Or if you like we could say: "0.1 is a BETTER solution than 0" because 123-1000*0.1 → 23 is smaller than 123-1000*0 → 123. If we were playing "Hot and Cold" we would be getting hotter! Then, let's zoom in even more, with a step of 0.01, and look at the interval from x=0.1 to x=0.2.
| x | 1000*x+7 | 130 | Equal? |
| 0.1 | 107 | 130 | false |
| 0.11 | 117 | 130 | false |
| 0.12 | 127 | 130 | false |
| 0.13 | 137 | 130 | false |
Overshoot again. Good, sort of... so now we look between x=0.12 to x=0.13, with a step of 0.01:
| x | 1000*x+7 | 130 | Equal? |
| 0.12 | 127 | 130 | false |
| 0.121 | 128 | 130 | false |
| 0.122 | 129 | 130 | false |
| 0.123 | 130 | 130 | true |
Bingo! The solution is x=0.123. Which means this zoom-in method to approximate the solution works. Cool... but that was way too long!
Drawing the solution
We can do better (and faster) than a table: we could turn a table into a drawing.
Here is the idea: take an equation that looks like an equivalence between two linear combinations, use a
coordinate system (AKA a sheet of squared paper with a couple of arrows crossing on it) to DRAW each linear combination, and look for where the two drawing cross (the math term is INTERSECT).
When I say that I want to "turn" a table into a drawing, I meant just that: let's turn the table on its side and create a rectangle for each value, to get a bar chart.
Let me take the (by now classic) example: 1*x+5 = 2*x+3 (spoiler!... the solutions is still x=2).
I want to take the table for 1*x+5, with values for
x that go from x=-3 to x=5, with step 1, and turn it on its side.
And since we are doing this, let's calculate also the table for
2*x+3,
in the same interval and turn it on its side as well.
|
-3→2
-2→3
-1→4
0→5
1→6
2→7
3→8
4→9
5→10
|
-3→-3
-2→-1
-1→1
0→3
1→5
2→7
3→9
4→11
5→13
|
And if we make the bars very thin, we will get two lines. Wait, so... when I draw a linear combination I get a straight line! I need of course to draw the two lines one on top of the other, AKA the two lines must be drawing in the same coordinate system (not side by side, as I did here).
Note: a great online tool, free, to draw math expressions (AKA to "plot" expressions) is FooPlot.
The diagram below was made with FooPlot, and it shows the two linear combinations 1*x+5, 2*x+3, and they meet where we expected, at x=2. The vertical axis is usually called the y axis, and what the plot shows is really the two lines:
y = 2*x+3
It is interesting to see that the two lines meet because they have different slopes, AKA they grow at different speeds. In these kinds of diagrams you typically look at the horizontal axis (the x axis) left to right, and as you follow the line (or lines) they might be going up or down, and that gives you the slope of the line.
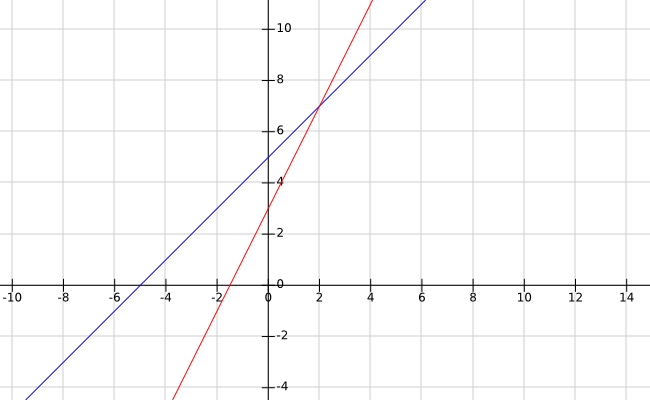
Moral of the story so far: riddles (AKA equations) can be written as sentences, represented by a two-pan balance, or written as an equivalence between two linear combinations. The solution to an equation can be found using an algorithm, and there are two special cases that we have to take into account. As an alternative to using the algorithm, we can look for the solution to an equation also by making a table (eventually a very detailed table, very annoying to calculate). It turns out that the table is easier to calculate if we draw its contents on squared paper (AKA a coordinate system). And when you draw a linear combination on a coordinate system you get a straight line; so an equation can be drawn as two lines. The solution to the equation lays where the lines meet (AKA where they intersect). Finally, the two special cases are: no solutions and infinite solutions. When the lines are parallel (they meet nowhere) we have zero solutions; and when the two lines are really the same line, any point on one of the lines is a good solution, hence, infinite solutions.
Now, try plotting the two special cases: 0*x=5, and 0*x=0.
Start from 1*x+5 = 2*x+3 and perform the steps required by the algorithm:
-1- move stuff around in the equation to get it to the form a*x=b,
-2- now divide by a to get the solution x=(b:a).
Plot the two lines after each step of the algorithm. You will get an animation of the way the algorithm solves an equation.
What happens to the two lines as the algorithm solves the equation?
What happens to the intersection point as the algorithm runs? Does it move? How?
Puzzles
(1) Solve riddles
Solve the following linear equations, using the final algorithm presented in this chapter.
- 5*x+10 = 2*x+46 → ?
- 7*x+7 = -8*x-2 → ?
- When I walk, I have to eat two candies every kilometer, for energy. However, before I start
my walk I always eat 3 candies, just to convince myself to get out of my house.
If I ate 11 candies in my last tour, how many kilometers did I walk?
The equation to solve here is: 3+2*x = 11, and x gives the kilometers walked. - 2*(4x+.3)-3x=45.6
- (3-x2)*2 = (10+x)-2*(x+2)
- 3*(x+x) = 1*2*3*4 + 6*x
- Alice can eat a whole cake in 4 minutes; Bob can also eat a whole cake, but it takes
him 6 minutes.
How long will it take to Alice and Bob together to eat one cake?
Here x is the time it takes to eat the whole cake.
14 + 16 = 1x
To help you I can rewriting the equation in this way:
14 + 16 = 1x → (14 + 16)*x = 1 assuming that x is not zero.
(2) Plot the solution
Using the plotting playground (the last one of the chapter) solve these equations:
- -14*x-18 = 16*x
- Can there be a number that divided by three times itself, becomes a third of itself? x:(3*x) = x3
- 9 = 1+2*x
(2.2) Plot the solution
Now go back to the playground called Build a riddle on a two-pan balance and solve the same equations, but with the two-pan balance this time. If needed, simplify the equation first, then solve them.Note: use FooPlot if you want a more flexible way to visualize, pan, zoom in and out.